The Pentagon That Could

It is a commonly known result that the regular pentagon cannot tile a 2D plane. This is in contrast to regular triangles, squares and hexagons, which do. However, it has been shown by Hirschhorn and Hunt, that many pentagonal tilings do exist, provided the pentagon is irregular, but equilateral. In other words, the lengths of the five sides are equal, but the angles are different.

Rotational symmetry

Of particular interest for the purposes of A5, is a pentagonal tiling which has a five-fold rotational symmetry. As shown in the aforementioned paper, such a tiling must have two non-adjacent angles 72° and 108°. With these fixed, all the other angles can be deduced from the fact that the sides are equilateral, as this example demonstrates.

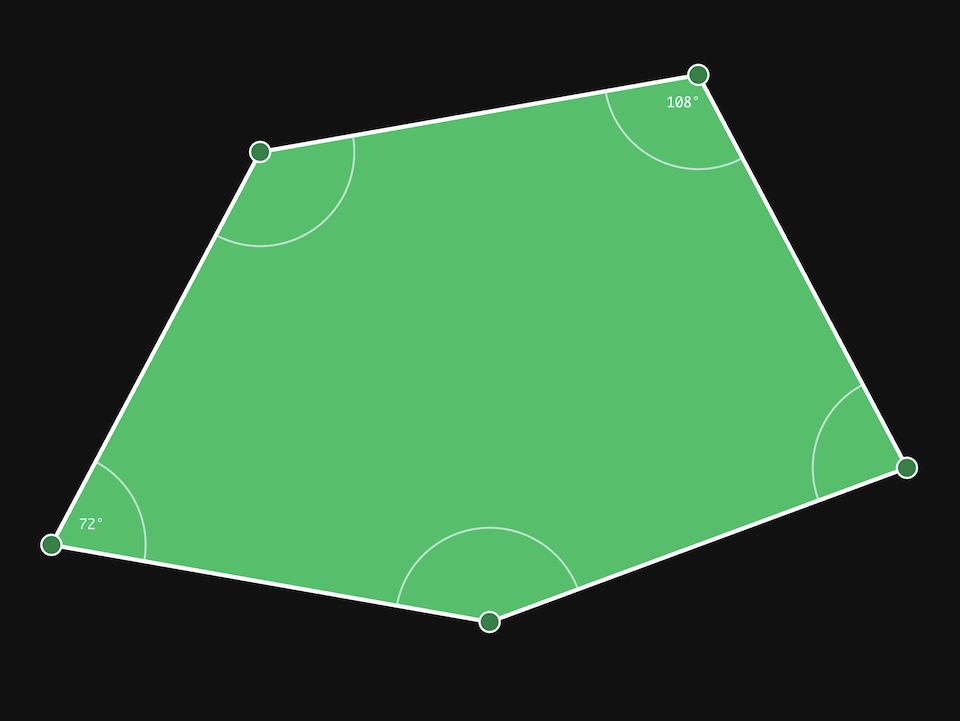
Constructing a lattice

By tiling this pentagon, a lattice is generated. As the size of the lattice grows the overall shape tends toward that of an isosceles triangle, with a vertex angle of 72°. By duplicating this tiling five times and rotating appropriately, a tiling is formed which has the shape of a regular pentagon.

The lattice can be explored in this example.