Skip to main content

Platonic Solids

In order to create a uniform grid of cells that covers the globe at different resolutions, the A5 system uses at each level:

  • A solid, which is the 3D shape of the whole grid,
  • A primitive, which is the shape of the cell used to construct the solid.

The primitives form a logical hierarchy, in that each primitive at a resolution level r + 1, has a parent primitive in the resolution level above it, r.

Note this hierarchy is purely logical, in general a primitive does not split geometrically into its children exactly. There is a high level of spatial coherence though, with children being co-located with their parents.

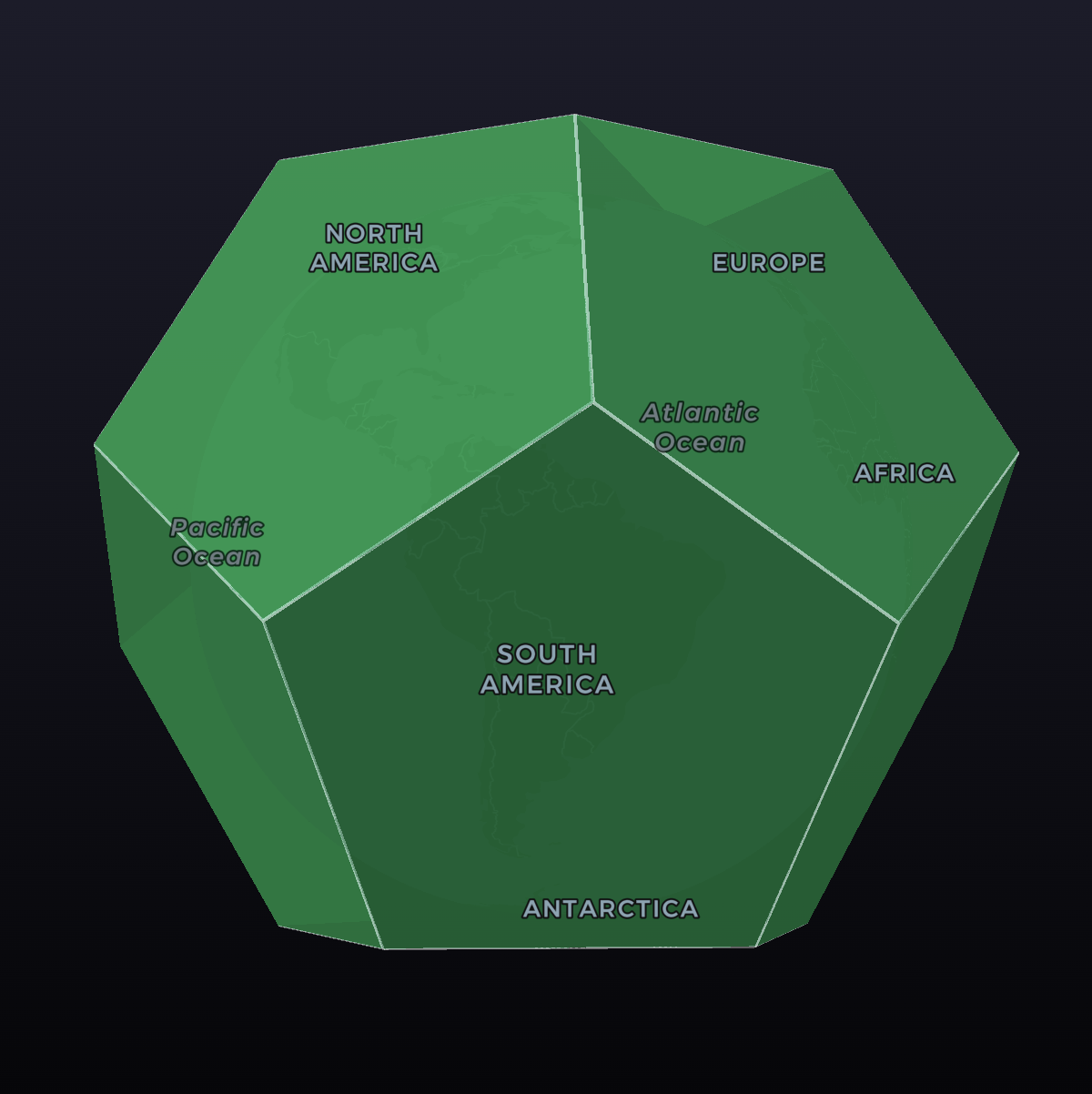
Resolution 0​

The first resolution level is simply the entire globe, with a single cell. Thus the primitive is a sphere and the solid is also a sphere.

Resolution 1​

For resolution 1, the globe is divided into 12 cells, with a regular pentagon as the primitive. Together, these form a solid regular dodecahedron, which is a Platonic solid.

The regular dodecahedron is the Platonic solid that most closely approximates a sphere, as it has the lowest angular defect at its vertices. It is this property that allows A5 to minimize the variation in cell size at all resolution levels.

Resolution 2​

The next resolution level subdivides each regular pentagon primitive into 5 icosceles triangles - yielding a total of 60 quintants. Together these form a solid pentakis dodecahedron. For clarity, the term quintant is used to refer to this primitive, as it forms a fifth of the pentagonal dodecahedron face.

Resolution 3​

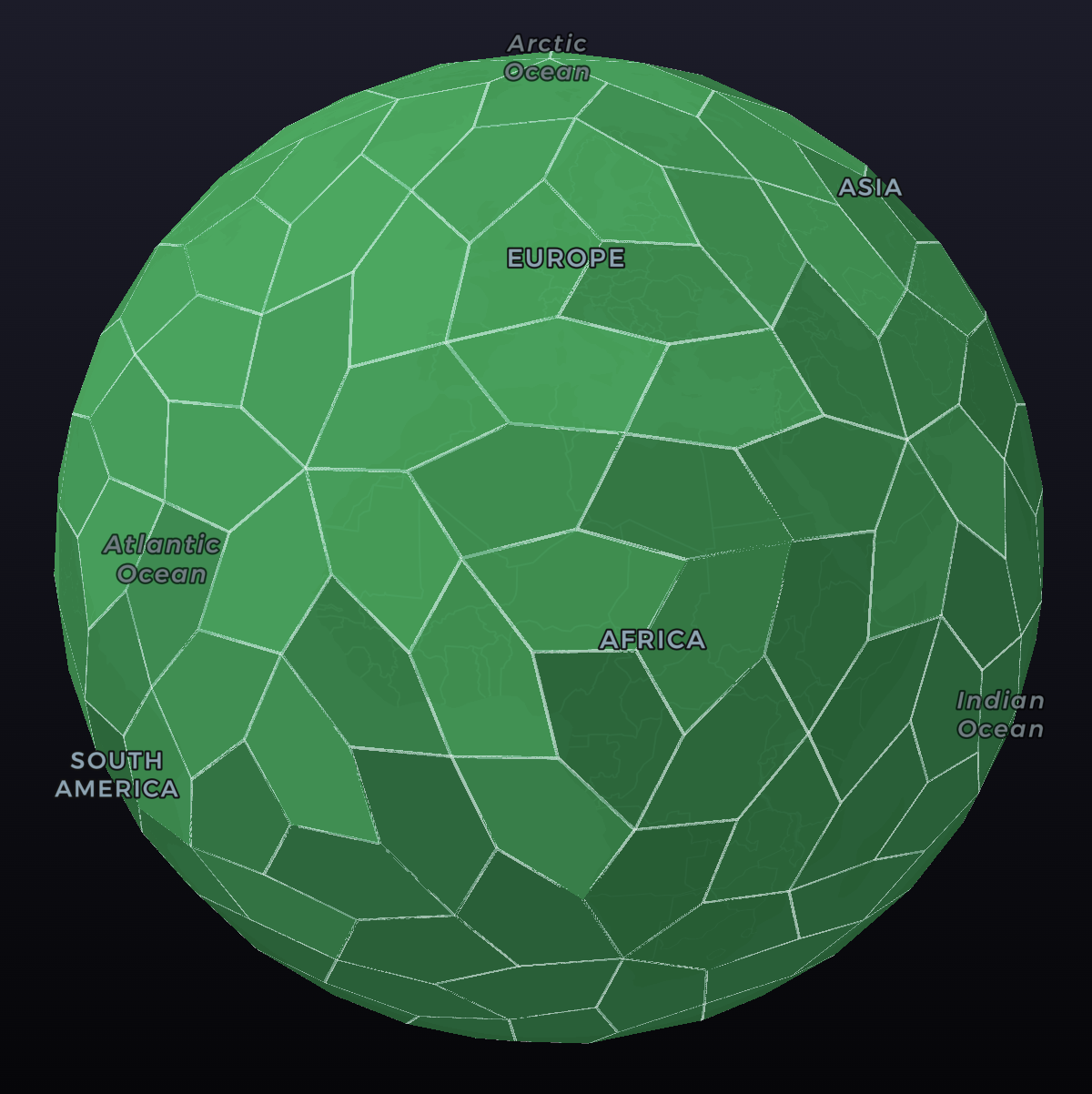
For higher resolution levels it is necessary to sub-divide each quintant primitive into smaller cells. This is achieved with a tiling using an irregular pentagon as a primitive, where each additional resolution level quadruples the number of cells. Thus resolution level 3 gives 240 cells, level 4 gives 960 cells and so on.

These cells together form a solid, which as far as the author is aware, has not yet been described and will be refered to as a teohedron.

While all the preceding solids have primitives of exactly equal shapes and sizes, the teohedron can be thought of as a pseudo-Platonic solid, in that it is constructed from primitives of almost equal shape and area (the area varies by only ~2%).

Resolution 4+​

All higher resolution levels are generated by using an ever-finer tiling using the irregular pentagon as a primitive. Even though the tiling forms a jagged edge (see example) along each side of the quintant, these edges perfectly mesh into each other, resulting in complete and uninterrupted coverage of the globe.

Two higher order teohedrons are shown below, which correspond to resolution levels 4 and 5.

In principle there is no limit to the resolution of a teohedron, however the A5 tiling system only uses finite number of resolution levels in order to store the cell identifier as a 64-bit integer.